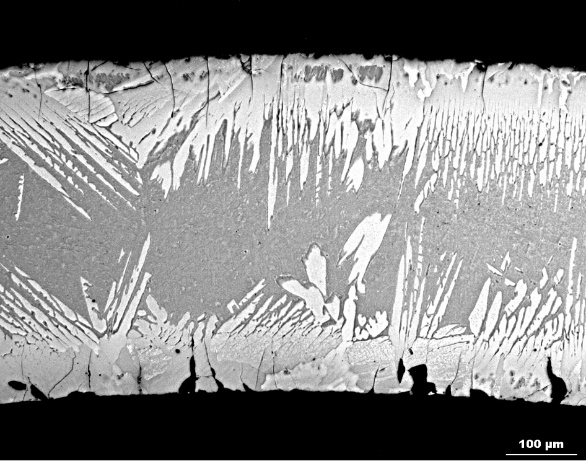Automatická segmentace obrazu je klasická úloha počítačové grafiky, jejímž cílem je vyznačit v obraze útvary, které označují jistý objekt či strukturu. Podle charakteru obrazu někdy postačí elementární metody založené na prahování barev, jindy je třeba vzít v úvahu vliv šumu, apriorní informaci o geometrii hledaného útvaru apod. K tomu existují metody založené na dynamice křivek, řešené pomocí parciálních diferenciálních rovnic [1] i moderní metody založené na strojovém učení a konvolučních neuronových sítích [2].
Účelem práce je seznámit se s vybranými metodami po teoretické i praktické (implementační) stránce a vyzkoušet jejich efektivitu na obrazech krystalické mikrostruktury na řezu pokrytí palivové tyče jaderného reaktoru. Toto pokrytí je vyrobeno ze slitin zirkonia a při podmínkách panujících v reaktoru, nebo hypotetických havarijních situacích dochází k oxidaci materiálu [3,4]. Vznikají velmi rozličné a komplikované struktury, kdy se vrstva oxidu prolíná s vrstvou kovu. Téma je vypsáno ve spolupráci FJFI se společností UJP PRAHA a.s., která realizuje výzkum v této oblasti a může poskytnout obrazová data získaná z experimentů bez přítomnosti paliva. Zapojení do uvedené tématiky otevírá perspektivu využití vyvinutých algoritmů i uplatnění absolventa v zajímavé inženýrské praxi.

Literatura:

[1] M. Beneš, V. Chalupecký, K. Mikula. Geometrical image segmentation by the Allen–Cahn equation, Appl. Num. Math 51 (2004), pp. 187-205, https://doi.org/10.1016/j.apnum.2004.05.001

[2] S. Minaee, Y. Boykov, F. Porikli, A. Plaza, N. Kehtarnavaz and D. Terzopoulos. Image Segmentation Using Deep Learning: A Survey, in IEEE Transactions on Pattern Analysis and Machine Intelligence 44 (7) (2022), pp. 3523-3542, https://doi.org/10.1109/TPAMI.2021.3059968.

[3] C. Schneider et al., Microstructural Analysis of Zirconia at the Fuel‑Cladding Interface in Medium and High Burnup Irradiated Fuel Rods. Oxidation of Metals (2021) 96:295–306, https://doi.org/10.1007/s11085-021-10045-8

[4] T. Sawabe et al, Microstructure of oxide layers formed on zirconium alloy by air oxidation, uniform corrosion and fresh-green surface modification. J. Nuclear Mater. 419 (2011), pp. 310-319, https://doi.org/10.1016/j.jnucmat.2011.05.028

Krystalická struktura materiálu má zásadní vliv na jeho mechanické vlastnosti. U nás ve skupině matematického modelování (MMG) má simulace procesů fázových přechodů v materiálech dlouhou tradici. Podrobně jsme se věnovali simulaci růstu krystalů a tvorby dendritických (chaotických rozvětvených) struktur při tuhnutí kovů. Podobně lze zkoumat procesy tání a nebo i komplikovanější procesy ve slitinách, jejichž primární hnací silou není přestup tepla (vznik tzv. martenzitických struktur). Pro matematický popis těchto procesů na úrovni kontinua (kdy nelze rozlišit jednotlivé částice) existuje několik přístpů, které lze použít: řešení úloh s volnou hranicí, vrstevnicová metoda (level set) nebo metoda fázového pole (phase field). Pro konkrétní fyzikální situace je potřeba zvolit vhodnou metodu, formulovat konkrétní matematický problém založený na soustavě parciálních diferenciálních rovnic a tento problém následně efektivně numericky řešit. Pokud je to možné, lze provést též matematickou analýzu problému, jejímž výsledkem jsou podmínky řešitelnosti soustavy a matematické vlastnosti jejího řešení.

Téma je dostatečně rozsáhlé pro práci v průběhu několika let. Student během své bakalářské práce pronikne do základů matematického modelování a numerické simulace některé jednoduché varianty problému. Pro názornost je vhodné formulovat problém nejprve ve dvou rozměrech, kde hranice mezi fázemi netvoří plochy, ale křivky. Dalším krokem je implementace numerického schématu, které tento problém řeší. V dalších letech (VÚ, DP) je možné přejít ke komplikovanějším variantám problému a zejména se věnovat implementaci numerických řešičů ve 3D, kdy značné výpočetní a paměťové nároky vyžadují použití paralelizace a neuniformních adaptivních numerických sítí.

Téma je vhodné pro studenty matematiky A, kteří se zároveň nebojí programování. Když se pustíte do práce, tak po chvíli pochopíte, k čemu v praxi ta matematika je :-)

Literatura:

[1] Beneš, M. Computational Studies of Anisotropic Diffuse Interface Model of Microstructure Formation in Solidification. Acta Math. Univ. Comenianae, 2007, 76, 39-59.

[2] Barrett, J. W.; Garcke, H. & Nürnberg, R. On Stable Parametric Finite Element Methods For The Stefan Problem and the Mullins-Sekerka Problem with Applications to Dendritic Growth. J. Comput. Phys., 2010, 229, 6270-6299.

[3] Strachota, P. Analysis and Application of Numerical Methods for Solving Nonlinear Reaction-Diffusion Equations. Dissertation, Czech Technical University in Prague, 2012.

[4] Strachota, P., Wodecki, A., Beneš, M.: Focusing the latent heat release in 3D phase field simulations of dendritic crystal growth. Modelling Simul. Mater. Sci. Eng. 29 065009 (2021).

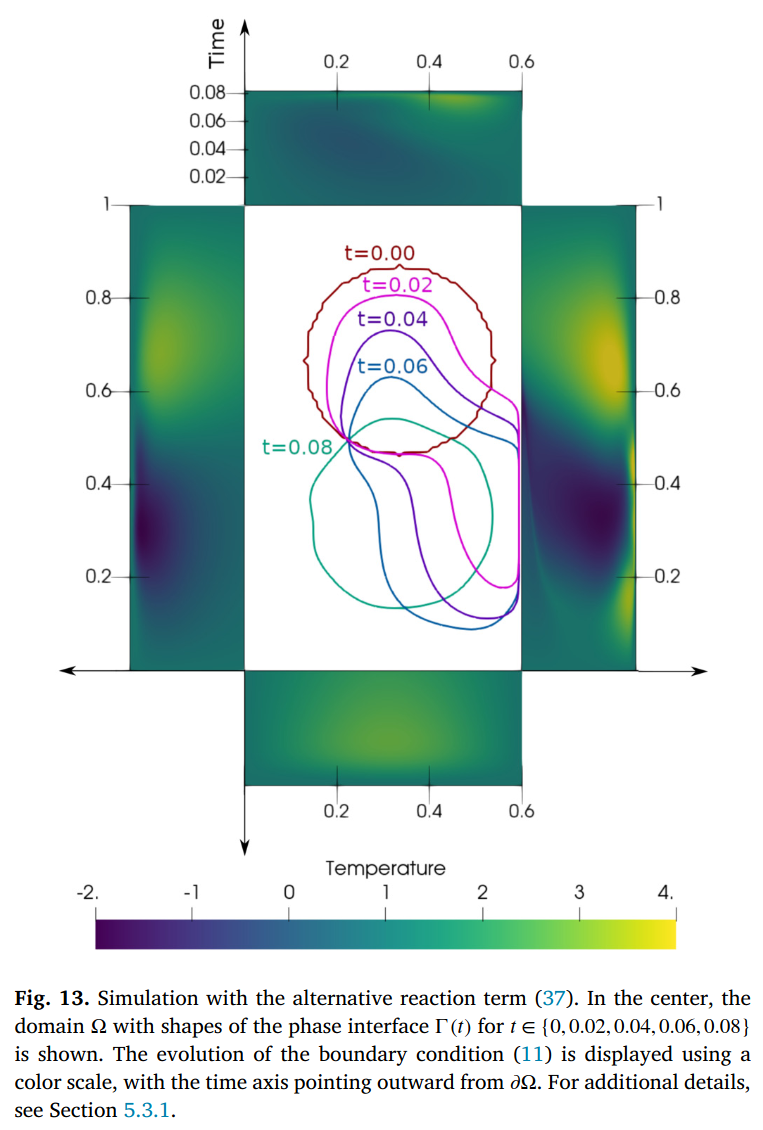Parciální diferenciální rovnice se užívají hojně k modelování přírodních jevů. Ať jde o rovnici vedení tepla nebo Schrödingerovu rovnici, zajímá nás, jak bychom mohli ovlivnit vývoj těchto procesů, aby probíhaly řízeně. Na tuto netriviální otázku lze často odpovědět s pomocí teorie řízení formulované na funkčních prostorech. Během své bakalářské/diplomové práce proniknete do vybraných partií teorie řízení. Teorii se naučíte aplikovat na problémy minimalizace funkcionálu s nekonečně dimenzionální vazbou. Tuto vazbu bude často představovat úloha pro diferenciální rovnici nebo systém diferenciálních rovnic. Vše formulujeme obecně pomocí funkcionálního počtu na Banachových nebo Hilbertových prostorech. Poté diskretizujeme problém minimalizace buď přímo, nebo užijeme duální úlohy odvozené na úrovni funkcionálního počtu, abychom navrhli efektivnější optimalizační řešič. Nakonec implementujeme navrženou metodu a ukážeme, že teoretická výstavba dává v praxi funkční způsob řízení fyzikálních procesů. Téma je vhodné pro studenty matematiky A, které zajímá praktický dopad pokročilejších partií matematiky (funkcionální analýzy) na řešení fyzikálních problémů.

Literatura:

[1] Wodecki, A., Strachota, P., Oberhuber, T., Škardová, K., Balázsová, M., Bohatý, M.: Numerical optimization of the Dirichlet boundary condition in the phase field model with an application to pure substance solidification. Comput. Math. Appl. 145 (2023), pp. 90-105, ISSN: 0898-1221, https://doi.org/10.1016/j.camwa.2023.06.007.

[2] M. Hinze, R. Pinnau, M. Ulbrich, and S. Ulbrich. Optimization with PDE Constraints. Springer, 2009.

[3] Luise Blank, Harald Garcke, Lavinia Sarbu, Tarin Srisupattarawanit, Vanessa Styles, and Axel Voigt. Phase-field approaches to structural topol- ogy optimization. In Constrained Optimization and Optimal Control for Partial Differential Equations, International Series of Numerical Mathematics vol. 160, pp. 245--256, Springer, 2012.

[4] J. Gao, B. Song, and Z. Mao. Combination of the phase field method and beso method for topology optimization. Struct. Multidisc. Optim. 61 (2020), pp. 225-237.

MMG spolupracuje s průmyslovými partnery na vývoji matematických modelů a simulačního softwaru pro komplexní procesy, v nichž významnou roli hraje (vícefázové) proudění tekutin. Příkladem je spalování uhlí a biomasy ve fluidních kotlích i v kotlích na práškové palivo. Kromě samotného proudění je nutné modelovat i řadu dalších jevů jako jsou chemické reakce při hoření, produkce a přenos tepla nebo interakce více fází v hořící směsi (plyn, částečky paliva, drcený vápenec). Sestavit výsledné rovnice je obtížný úkol vyžadující dobrou znalost matematiky i inženýrský „cit“. S ohledem na aplikaci výsledků simulací je totiž třeba činit vhodné kompromisy mezi složitostí modelu, úrovní detailů, přesností, výpočetní náročností a dalšími aspekty. Výsledné modely mají víceškálový (multiscale) charakter, který klade vysoké nároky na vlastnosti a efektivitu numerického řešiče. Proto často používáme paralelní implementace pracující na výpočetních clusterech. Modely a numerické algoritmy je třeba verifikovat (ověřit správnou funkci pomocí standardních testů) a validovat (srovnat výsledky s reálnými naměřenými hodnotami).

Kromě "populárního" spalování v kotlích, které rádi ukazujeme na různých seminářích pro studenty, lze velmi podobně přistupovat i k řešení dalších problémů. Z poslední doby máme zkušenosti s modelováním proudění a kondenzace ve výfukovém potrubí automobilů a s modelováním dynamiky Li-ion akumulátorů. V průběhu řešení průmyslových projektů jsme se zabývali všemi výše popsanými aspekty daných problémů, avšak každý z nich by si rozhodně zasloužil pečlivější rozbor a studium. Budeme velmi rádi, když nám s tím pomůže někdo z Vás, talentovaných studentů :-) Téma je dostatečně rozsáhlé pro práci v průběhu několika let, od bakalářské práce po práci diplomovou, a případně i v doktorském studiu.

Literatura:

[1] Anderson, J. D. Computational Fluid Dynamics: The Basics with Applications. McGraw-Hill, 1995.
[2] Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Description. Academic Press, 1994.
[3] Cengel, Y. A. & Boles, M. A. Thermodynamics: An Engineering Approach. McGraw-Hill, 2006.
[4] Kolev, N. I. Multiphase Flow Dynamics 2: Mechanical Interactions. Springer, 2011.
[5] Kolev, N. I. Multiphase Flow Dynamics 3: Thermal Interactions. Springer, 2011.
[6] Basu, P.; Kefa, C. & Jestin, L. Boilers and Burners: Design and Theory. Springer, 1999.

Kryptoměny mají do značné míry spekulativní povahu a obchodování s nimi není tolik ovlivněno vnějšími faktory, jako je to na burzách akcií. Kryptoměnové burzy nabízejí ruční zadávání příkazů přes webové rozhraní, avšak rozhodnutí nakoupit či prodat je jako sázení loterie. Kromě toho lze využít aplikační rozhraní (API) pro obchodování a s jeho pomocí vytvářet automaticky obchodující (ro)boty. Robot obvykle uplatňuje pevně naprogramovanou tzv. strategii, a obvykle prodělává. Není však možné díky odtrženosti kryptoměn od reálné ekonomiky vypozorovat v obchodování složitější vzory chování, které by umožnily predikovat budoucí vývoj a vyvinout výdělečnou strategii? A bylo by možné k tomu využít hluboké neuronové sítě (deep neural networks)?

V rámci dané práce bychom se pokusili prozkoumat, zda je vůbec nějaká šance na úspěch. Ve hře je nejen návrh architektury neuronové sítě, ale také výběr vstupních dat, časového rámce pro jejich sběr, a především otázky, na kterou má neuronová síť odpovědět. Například existují sítě, které umí predikovat budoucí vývoj (tvar křivky) ceny na základě historických dat. Predikce tak obsahuje spoustu informace, ale její úspěšnost je nepatrná. Jde to udělat chytřeji?

Práce nabízí příležitost porozumět metodám strojového učení a zejména fungování hlubokých neuronových sítí. Dále si student osvojí programátorské schopnosti a práci v Linuxu z uživatelské (překvapivě) i administrátorské stránky. Bonusem je náhled do fungování finančních trhů a samozřejmě vidina pohádkového zbohatnutí :)

Veškeré analýzy lze provádět na historických i veřejně dostupných aktuálních datech.

Literatura:

[1] C. C. Aggarwal - Neural Networks and Deep Learning, Springer, 2018.

[2] F. Chollet - Deep Learning with Python, Manning Publications Co., 2018.

[3] G. Zaccone, R. Karim - Deep Learning with TensorFlow, Packt Publishing, 2018.

[4] S. Pattanayak - Pro Deep Learning with TensorFlow, Apress, 2017.

[5] K. Söze - Bitcoin and Cryptocurrency Technologies. Sabi Shepherd Ltd., 2019.

Akciové trhy poslední dobou zažívají nebývale bouřlivé období. Do ekonomiky se v rámci vládních podpůrných programů dostává obrovské množství peněz, zvyšuje se inflace a do investování či obchodování s akciemi se pouští mnoho malých investorů, kteří nemají zkušenosti. Řada fondů ovšem dokazuje, že aktivním řízením portfolia, tj. vhodně zvolenými a načasovanými operacemi lze získat výnos, který významně předčí růst trhu. Jejich obchodní strategie jsou přitom založeny v zásadě na dvou principech: technické analýze, která hledá vzory či závislosti výlučně v historickém cenovém vývoji, a fundamentální analýze, která využívá k obchodním rozhodnutím aktuálních i historických údajů z reálné ekonomiky, politiky a obecně života lidské společnosti. Úspěšný obchodník musí nejen mít přístup k fundamentálním datům, ale též umět určit, která data jsou pro jeho obchodní strategii podstatná, a pokud jsou, tak jakým směrem, v jakém časovém horizontu a jak výrazně ovlivňují pohyb cen akcií, s nimiž obchoduje.

Tyto otázky se pokusíme zodpovědět v naší práci za pomoci klasických statistických metod (např. PCA) i metod strojového učení (zejména neuronových sítí). Analyzovaná data budou nejprve syntetická, avšak díky spolupráci se subjektem pohybujícím se v oboru lze posléze využít i rozsáhlé databáze reálných historických fundamentálních dat o veřejně obchodovaných společnostech na burze v USA (např. obrat, zisk, výše dluhu, cash-flow, prodeje zboží/služeb atd.) a příslušných dat o ceně akcií. Práce obnáší seznámení s matematickým pozadím i praktickými softwarovými nástroji strojového učení, implementaci modelů a jejich testování. Důležitá bude i kreativita a intuice. Lze například kombinovat více metod, kdy v první fázi se vyloučí silně korelované parametry, a v dalším zpracování se podmnožina původních dat podrobí náročnější analýze s cílem najít univerzální závislosti platné nezávisle na zvoleném časovém období.

Téma má potenciál vývoje od bakalářské práce až po práci diplomovou.

Literatura:

[1] C. C. Aggarwal - Neural Networks and Deep Learning, Springer, 2018.

[2] T. Hastie, R. Tibshirani, J. Friedman – The Elements of Statistical Learning, Data Mining, Inference, and Prediction. 2nd. ed., Springer-Verlag New York, 2009.

[3] A. C. Müller, S. Guido – Introduction to Machine Learning with Python, A Guide for Data Scientists. O‘Reilly, 2016.

[4] F. Chollet - Deep Learning with Python, Manning Publications Co., 2018.

[5] S. Pattanayak - Pro Deep Learning with TensorFlow, Apress, 2017.

Řada objektů nebo scén má na první pohled velmi složitou geometrii, kterou však lze alespoň přibližně popsat relativně jednoduchými formálními pravidly nebo algoritmy. Jako příklad lze uvést rostliny nebo celé ekosystémy (louka, les), hornatý terén, oblaky, rozvlněnou vodní hladinu, města s pravoúhlou sítí ulic, lidský dav atd. Tyto objekty a scény často mají do jisté míry fraktální povahu. Chceme-li vytvořit jejich počítačový model, je možné analyzovat jejich strukturu a navrhnout algoritmus, který (často s využitím rekurze a náhodnosti) tento model automaticky vygeneruje. Tomuto přístupu se říká procedurální modelování, které obecně má dvě fáze:

1. V první fázi jde o vygenerování abstraktního popisu objektu (např. strom se skládá z kmenu, větví, listů, květů atd.) s použitím vhodného formalismu (např. D0L systémy), který se uloží do odpovídající datové struktury.
2. Následně jsou tato data použita pro vytvoření samotné geometrie objektu a k jeho otexturování.

Nakonec je nutné objekt vhodným způsobem vizualizovat (vyrenderovat), případně jej uložit do formátu, který bude možné zpracovat dostupnými vizualizačními nástroji nebo knihovnami.

V současnosti existuje nepřeberné množství algoritmů procedurálního modelování. Téma je vhodné pro kreativní studenty matematické informatiky nebo softwarového inženýrství, kteří jsou schopni samostatně studovat literaturu, vyhledávat si zdroje, a zároveň je baví programování. Lze si vybrat libovolný typ objektu, udělat si přehled o metodách jeho procedurálního modelování, implementovat nejprve ty základní a dále je vylepšovat s použitím literatury i vlastních nápadů. Při práci student využije a zdokonalí své dovednosti z matematiky, programování, teoretické počítačové grafiky, stejně jako vlastní fantazii. Mimo to by si měl procvičit správné postupy při tvorbě softwarového projektu.

Literatura:

[1] Prusinkiewicz, P., Lindenmayer, A. The Algorithmic Beauty of Plants. Springer-Verlag, 1990. ISBN 978-0387972978.

[2] Kelly G., McCabe H. A Survey of Procedural Techniques for City Generation. ITB Journal (14), 2006, pp. 87-130.

[3] Smelik R. M., de Kraker K. J., Tutenel T., Bidarra R., and Groenewegen S. A. A Survey of Procedural Methods for Terrain Modelling. In Proceedings of the CASA Workshop on 3D Advanced Media In Gaming And Simulation (3AMIGAS), Amsterdam, The Netherlands, June 2009.

Na katedře matematiky společně s katedrou inženýrství pevných látek provozujeme výpočetní svazek (cluster) pro paralelní vysoce výkonné výpočty (HPC - High Performance Computing), který neustále rozšiřujeme. Stejně tak stoupá počet jeho uživatelů. Tento stále složitější systém již vyžaduje profesionální softwarová řešení, používaná i v předních světových výpočetních centrech. Student, který si zvolí toto téma, se postupně seznámí se specifickými problémy při stavbě a provozování výpočetního clusteru, od volby a nastavení hardwaru a operačního systému přes konfiguraci distribuovaného systému souborů až po nasazení softwaru pro zpracování úloh (job scheduler). Všechny systémy lze bezpečně testovat s pomocí virtualizačních nástrojů, které jsou dnes již volně k dispozici. V pokročilejších stádiích práce student analyzuje možnosti více dostupných řešení a navrhne funkční softwarovou konfiguraci výpočetního svazku. Získané zkušenosti bude možné uplatnit při konfiguraci existujících reálných systémů.

Nově se otevírá možnost využít cluster HYPERION (672 jader AMD Opteron, 1600 GB RAM), který bude uveden do provozu na podzim 2015. Místo na konfiguraci softwaru se lze zaměřit na návrh paralelních algoritmů numerické matematiky, jejich implementaci a zlepšování jejich efektivity (na základě poznatků z profileru). Za tímto účelem se nabízí celá řada  možností (hybridní paralelizace, vyvažování zátěže, optimalizace přístupů do paměti a využití cache, optimalizace komunikace, pevné vazby procesů na výpočetní jádra atd).