Taylorovy polynomy zadané funkce: exp(x)
| > | # initialize
restart; with(plots); f:=exp(x); # nmax is the maximum approximation order (the order of the Taylor polynomial + 1) nmax:=7; setoptions(thickness=2); |
|
|
|
|
|
(1) |
| > | # initialize the lists T and R
T:=[seq(0,i=1..nmax+1)]; R:=T; # now calculate the Taylor polynomials for n from 1 to nmax do T[n]:=convert(taylor(f,x,n),polynom); R[n]:=f-T[n]; end do; n:='n'; |
![[0, 0, 0, 0, 0, 0, 0, 0]](taylor-approximation-exp-images/taylor-approximation-exp_10.gif){kind=small} |
|
![[0, 0, 0, 0, 0, 0, 0, 0]](taylor-approximation-exp-images/taylor-approximation-exp_11.gif){kind=small} |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
(2) |
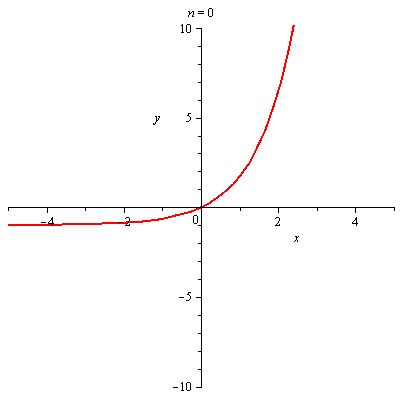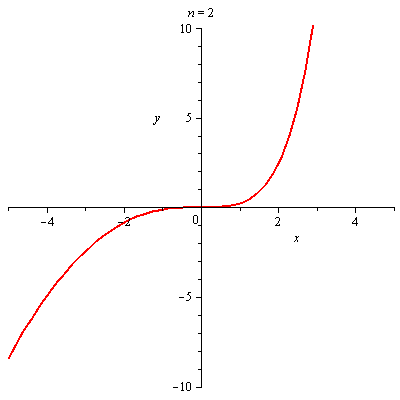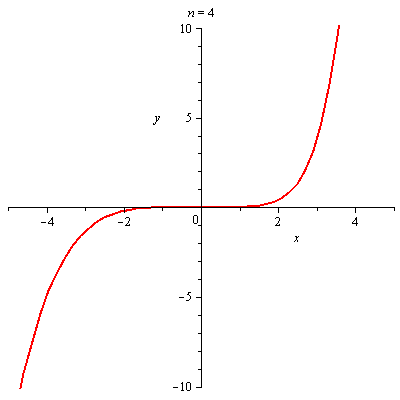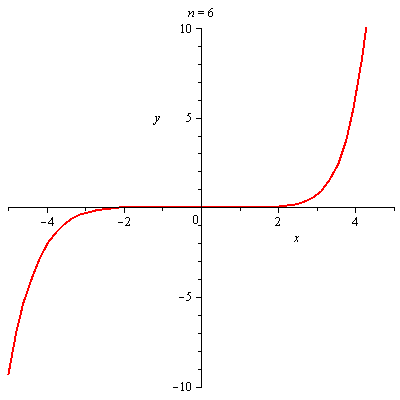
Graf funkce a jejího n-tého Taylorova polynomu
| > | # n goes from 0 to nmax-1 to represent the order of the Taylor polynomial
plots[animate](plot,[[f,T[n+1]],x=-5..5,y=-10..10],n=[seq(i,i=0..nmax-1)]); |
 |
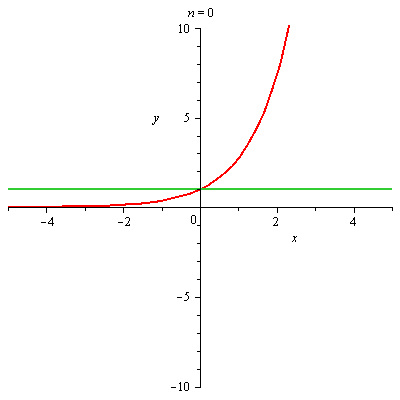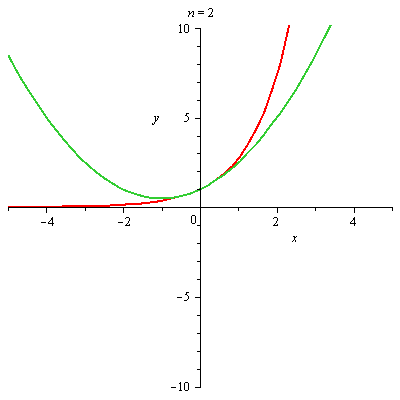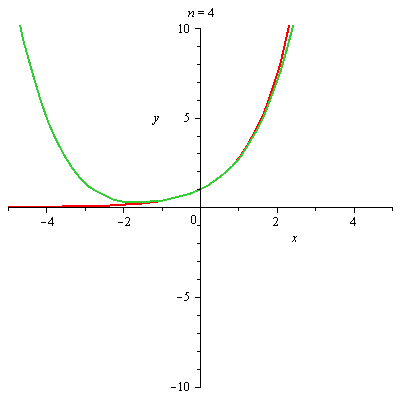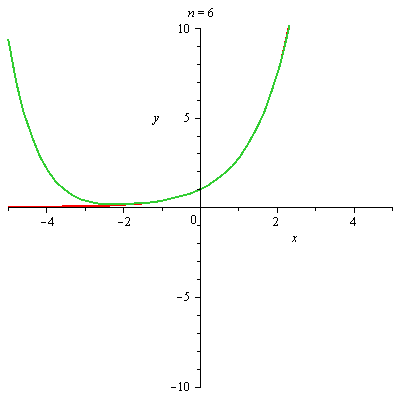Graf zbytku po n-tém Taylorově polynomu
| > | animate(plot,[R[n+1],x=-5..5,y=-10..10],n=[seq(i,i=0..nmax-1)]); |
 |
| > |