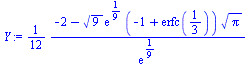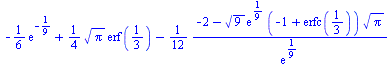Příklad 8.6 - přibližný výpočet π pomocí prvních 6 nenulových členů rozvoje arctg(1) a arcsin(1/2) 

>	pi_approx:=4*sum((-1)^n/(2*n+1),n=0..5);

 

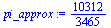(1)

 

>	evalf(pi_approx); evalf(Pi-pi_approx);

 

 

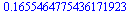	(2)

 

Odhad chyby pomocí následujícího členu alternující řady 

>	evalf(4/(2*5+1));

 

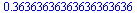(3)

 

>	pi_approx2:=6*sum(doublefactorial(2*n-1)/(doublefactorial(2*n)*(2*n+1))*(1/2)^(2*n+1),n=0..5);

 

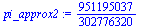(4)

 

>	evalf(pi_approx2); evalf(Pi-pi_approx2);

 

 

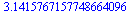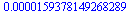	(5)

 

Odhad chyby pomocí součtu zbytku řady (odhadnutého shora součtem geometrické řady) 

>	evalf(6/13*sum((1/2)^(2*n+1),n=6..infinity));

 

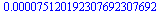(6)

 

Příklad 8.7 - přibližný výpočet integrálu 

>	int(ln(1+x^2),x=0..1);

 

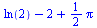(7)

 

>	sum((-1)^(n+1)/(n*(2*n+1)),n=1..infinity);

 

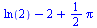(8)

 

Příklad 9.1 - přibližný výpočet a odhad chyby 

>	X:=int(x^2*exp(-x^2),x=0..1/3);

 

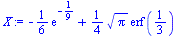(9)

 

>	Y:=sum((-1)^n/n!*(1/3)^(2*n+3)/(2*n+3),n=0..infinity);

 

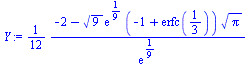(10)

 

>

X-Y;

 

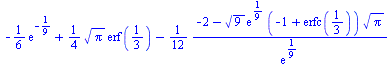(11)

 

>	simplify(X-Y);

 

(12)

 

Aproximace pomocí prvních n0+1 členů sumy 

>	n0:=3; Y_approx:=sum((-1)^n/n!*(1/3)^(2*n+3)/(2*n+3),n=0..n0);

 

 

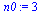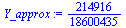	(13)

 

Při počítání s malou přesností bychom mohli dostat nesprávné výsledky, zdánlivě větší než je odhad... 

>	Digits:=8; evalf(Y-Y_approx);

 

 

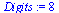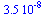	(14)

 

Zvětšíme přesnost a výsledek se podstatně změní 

>	Digits:=20; evalf(Y-Y_approx);

 

 

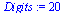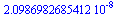	(15)

 

Na kolik míst umíme vlastně maximálně počítat? 

>	kernelopts(maxdigits);

 

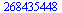(16)

 

To snad bude stačit... Odhadneme chybu pomocí dalšího členu alternující řady: 

>	1/(n0+1)!*(1/3)^(2*(n0+1)+3)/(2*(n0+1)+3);

 

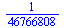(17)

 

>

evalf(%);

 

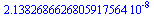(18)

 

To je o trochu víc než je skutečná chyba.